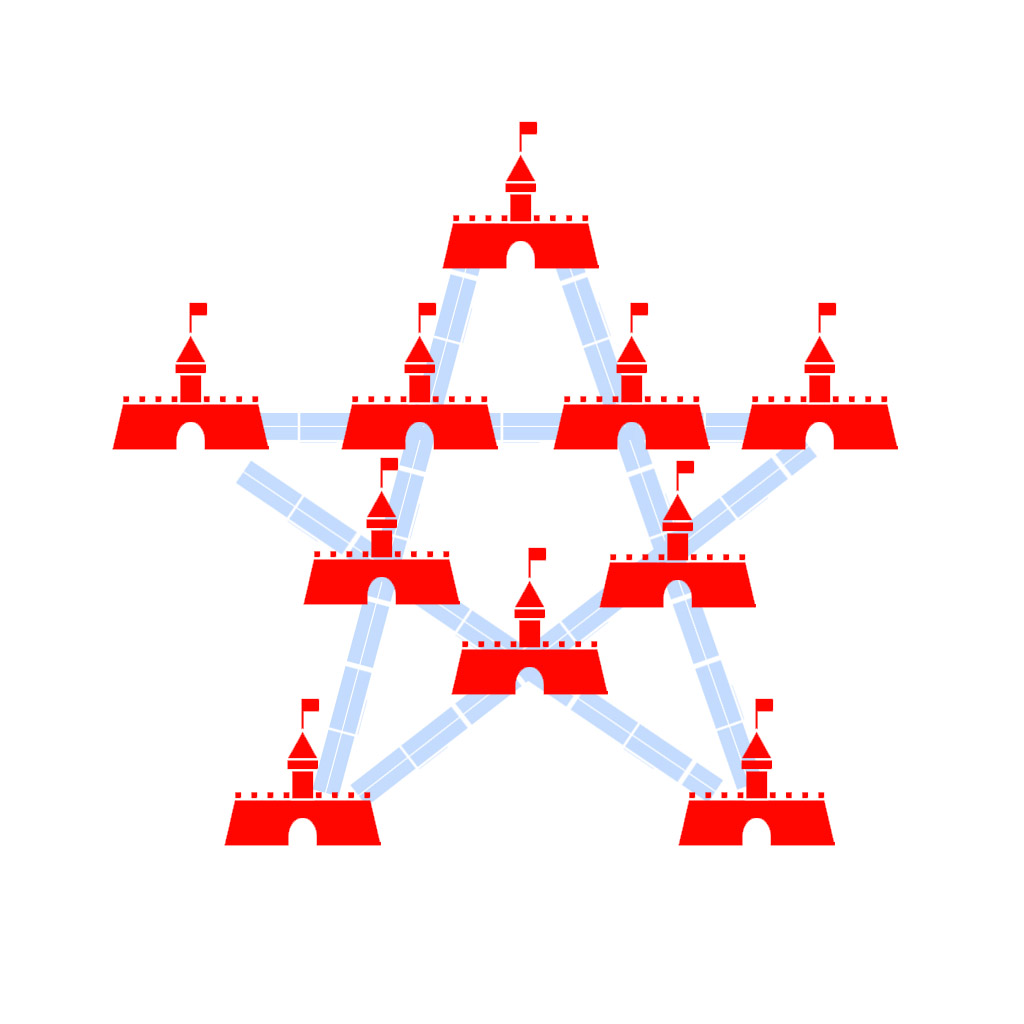
A time long back, there lived a king who ruled the great kingdom of Trojan House. As a part of the renovation of the kingdom to meet future security needs, he asked his chief architect to lay down a new play in a manner that all of his 10 castles are connected through five straight walls and each wall must connect four castles together. He also asked the architect that at least one of his castles should be protected with walls. The architect could not come up with any solution that served all of King's choices, but he suggested the best plan that you can see in the picture below. Can you find a better solution to serve the king's demand?

There are three boxes of different sizes with three cupcakes inside each of the boxes in Christina's kitchen. At night her daughter wakes up and goes to the kitchen. She opens a box and eats all three cakes.

But in the morning Christina finds out that each box still had three cupcakes. How?

If 1+9+8=1, what is 2+8+9?

What word is represented by this rebus?

The chance of Mr John winning the lottery is 10%. All participants lined up and Mr John is 4th in the row. The first three participants lose the lottery.

What is the chance of Mr John now?

Jigsaw captured 100 people and make them stand in a circle and all these people are labelled as Person1, Person2, Person3... Person100. He made them play a crazy game in which Person 1 shot Person 2 and pass the gun to the next person and so on until one stands alive.

Which person will survive in the end?

An artist while painting a scenic beauty, decides to paint three layers of blue colour on the sky.

Which layer will go on the first?

Can you name an animal whose killing cannot be performed without spilling your own blood?

Can you name three consecutive days without using the words Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, or Sunday?

Can you find the key in the picture below?